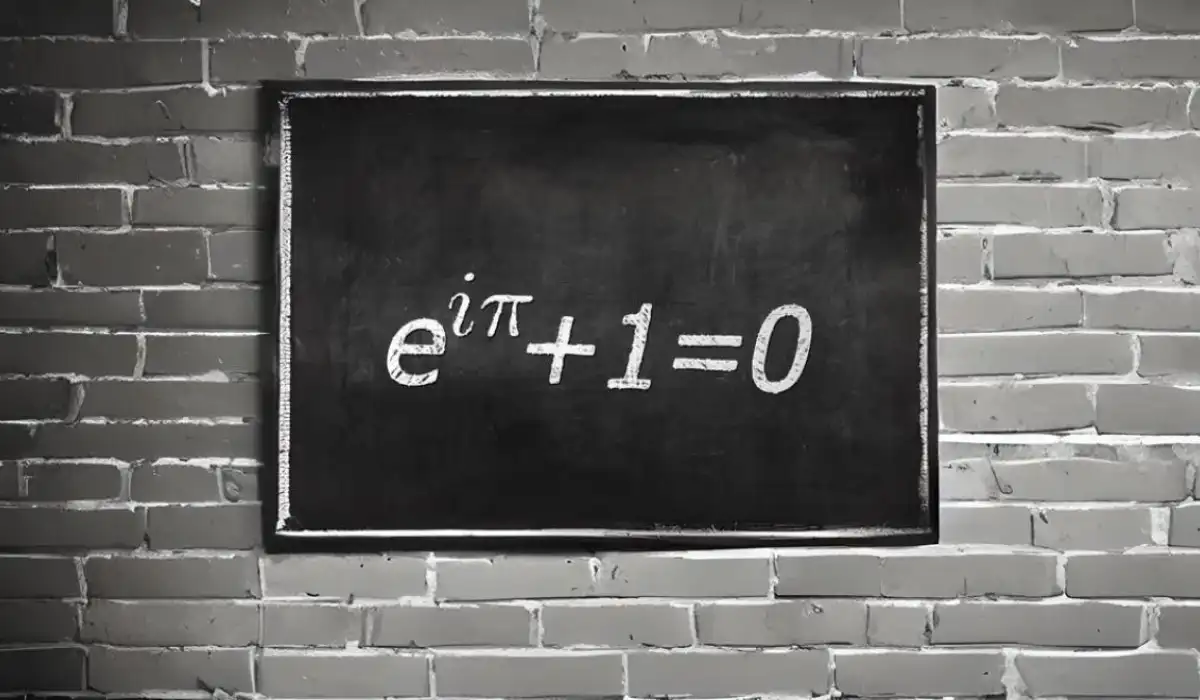Observing E-Day, also recognized as Euler’s Number Day, is a celebration of the constant e in mathematics, which is roughly the equivalent of 2.71828. This distinct figure is a fundamental element in a variety of mathematical subjects, including calculus and complex numbers, as well as numerous applied mathematics applications.
E-Day is celebrated on February 7th, symbolizing the loose value of e when represented in a date format. Comparable to Pi Day, E-Day pays tribute to essential mathematical ideas while also making the subject more engaging and accessible to the public.
History of e-Day
The mathematical constant e, also known as Euler’s number, is a transcendental number that is the base of the natural logarithm. The number e itself is approximately equal to 2.71828, though its digits continue indefinitely without repeating.
The constant e was first used in calculus, although its earlier existence can be traced back to John Napier’s invention of logarithms in the early 17th century. The roots of e can be seen in his work when he introduced a logarithmic base that was approximately equal to 0.9999999, which corresponds to 1/e.
In the mid-18th century, the Swiss mathematician Leonhard Euler developed the use and concept of e in calculus. He named the constant after himself, although it is also known as the base of the natural logarithm.
Euler was the first to make extensive use of the constant, and he proved that e is an irrational number (cannot be expressed as a simple fraction) and that it is also transcendental (is not a root of any non-zero polynomial equation with integer coefficients).
Over the years, the number e has taken a prominent place in mathematics, especially in calculus and complex analysis, due to its unique properties. The constant e appears naturally in many mathematical models and formulas describing growth and decay, and in other scenarios involving compound interest or the calculation of probabilities, among many other applications.
e-Day Timeline
First References to the Constant
John Napier published the first references to the constant in an appendix of his work on logarithms.
Introduction of the Constant
Jacob Bernoulli introduced the constant for solving the problem of continuous compounding of interest.
Euler Begins Using the Letter e
Leonhard Euler started using the letter e for the constant in an unpublished paper on explosive forces in cannons.
First Printed Appearance of e
The first appearance of the letter e in a printed publication was in Euler's Mechanica.
Euler's Formula
Euler links the constant e to complex numbers, forming the basis of Euler's formula.
Use of e in Various Fields
e is indispensable in many fields, including calculus, number theory, and complex analysis. It's also widely used in physics, engineering, and computer science.
Ideas to Celebrate e-Day
Euler's Number Workshop
Invite a knowledgeable guest speaker in the field of mathematics to conduct an expressive workshop highlighting Euler's number. This can include enlightening discussions or straightforward demonstrations that make learning math enjoyable.
Visit a Science Museum
Organize a group visit to a science or mathematics museum, preferably one that exhibits related to mathematical constants. It would provide a fresh perspective and knowledge base about the importance of 'e' in a real-world setting.
E-Day Appreciation Post
If you manage a blog or social media, write an appreciation post on E-Day, divulging fascinating facts about the application and relevance of the constant 'e'. It will help your followers discover the brilliance of mathematics.
Interview a Mathematician
Arrange for a mathematician or a lecturer at a university to appear on a video call on E-Day. The call can be about the mathematician explaining the applications and significance of the number 'e' in an accessible language.
E-day Math Project
Start a mathematical project centered around 'e', like calculating growth rates or compound interest. This project can be a fun way for both children and adults to engage with the number 'e', understanding its importance in mathematics.
7 Interesting Facts About e
Named by Euler
The constant e, associated with natural logarithms, was christened by Leonhard Euler, a Swiss physicist and mathematician, during the 1700s.
Transcendental Number
E bears the status of being a transcendental number. This implies that no non-constant polynomial equation formulated with integer coefficients can have e as a solution. Pi and specific cosine function values are other popular transcendental numbers.
Unlimited Decimal Expansion
Similar to pi, e is an irrational number that possesses an endless decimal expansion with no observable repetition or pattern.
Golden key to calculus
e^x as a function behaves uniquely by being its own derivative in calculus. This uniqueness transforms e into an essential element in calculations, especially while working with exponential decay or growth matters.
Growth Formula
e has a role in the formula of continuous compounding popular in finance to calculate an investment's future value. The formula, A = P * e^(rt), sets 'P' as the principal sum, 'r' as the interest rate, 't' as the period, and 'A' as the money sum that will be amassed after 't' years at an annual interest rate of 'r', compounded continuously.
Normal Distribution Constant
e stands as the foundation of standard normal distribution or the bell curve utilized widely in statistical analysis.
Base for Natural Logarithms
Mathematics designates the logarithm with e as its base as the natural logarithm, signified by 'ln'. It has massive applications in many mathematics branches such as calculus, analysis, and complex numbers.
e-Day FAQs
Next e-Day Dates
| Year | Date | Day |
|---|---|---|
| 2023 | February 7th | Tuesday |
| 2024 | February 7th | Wednesday |
| 2025 | February 7th | Friday |
| 2026 | February 7th | Saturday |
| 2027 | February 7th | Sunday |
| What is the pattern? | Every February 7th | |
e-Day Word Search
- Exponent
- Constant
- Euler
- Natural
- Logarithm
- Irrational